ti-89 | mathe | parabel()	Download
Beschreibung Dieses Programm dient der Berechnung von Parabeln deren Hauptachsen parallel zur Y- Achse liegen
Screenshots
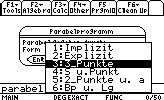
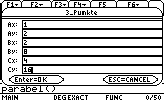
Anleitung Um die Parabel berechnen zu können muss man entweder die Parameter der Parabelgleichung... ax2+bx+c=y; a, b und c sind bekannt y=a(x-u)2+v oder y-v=a(x-u)2; a, u und v sind bekannt ...oder die Koordinaten gewisser Punkte, kennen: Drei Punkte der Parabel: (A(xa,ya);B(xb,yb);C(xc,yc);) Die Koordinaten des Scheitelpunktes (S(u,v)) und eines weiteren Punktes Die Koordinaten zweier Punkte (A(xa,ya);B(xb,yb)) und die Breite der Parabel (a) Die Koordinaten des Brennpunktes und die Gleichung der Leitgeraden (z.B. 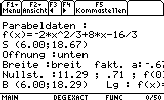y=3) Das Programm gibt eine Funktionsgleichung (z.B. y=2x2+3x-7) normalerweise in der Form y=ax2+bx+c, bei impliziter Eingabe jedoch in der Form y=a(x-u)2+v aus. Zusätzlich werden folgende Grössen berechnet: die Koordinaten des Scheitelpunktes, (S(u,v)) die Öffnung (oben und unten) die Breite (schmal, normal, breit) a (als Zahlwert) die Nullstellen der Funktionswert für x=0 (Also Schnittpunkt mit der y- Achse) die Koordinaten des Brennpunktes (Bp(xbp,ybp)) die Gleichung der Leitgeraden (in der Form y=) Die Ausgabe erfolgt entweder exakt (z.B. 25/17) oder Gerundet auf vier Nachkommastellen (z.B. 3.5714). Zusätzlich besteht die Möglichkeit, die Parabel zu zeichnen [F2]. Hierbei kann es vorkommen, dass die Parabel ausserhalb des Fensters liegt, sodass man einen weissen Bildschirm vor sich hat. In der nächsten Version wird man deshalb die Möglichkeit haben, die Fenstergrösse zu verändern.