Hyperbolic perpendicular line
The construction of hyperbolic perpendicular lines. As usual this is done via the intersection of
two circles.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
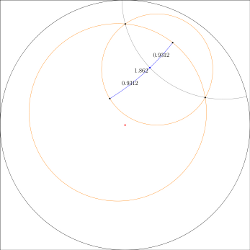
Hyperbolic midpoint
Construction of a hyperbolic midpoint. This works the same as in the euclidean case.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
Angle bisection
Construction of a angle bisecting line. This works the same as in the euclidean case.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
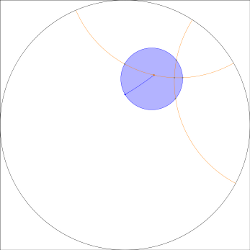
Center of circle
The classical construction for finding the center point of a circle.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
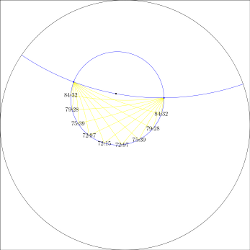
Theorem of Thales
The theorem of Thales does not hold in the hyperbolic plane.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
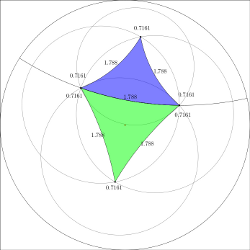
Equilateral triangle
An equilateral triangle construction.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
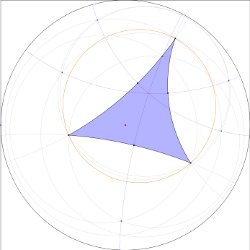
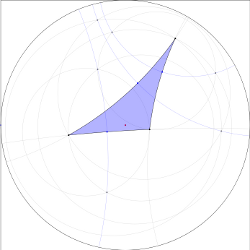
Circumcircle of a hyperbolic triangle
The constructoin of a circumcircle does in principle work, but sometimes the
the lines do not intersect thus the midpoint can not be found.
 Rendered as .pdf
Rendered as .pdf
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
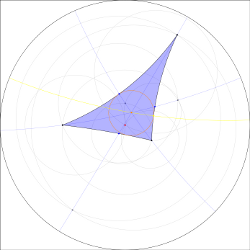
Incircle of a hyperbolic triangle
Construction of an incircle of an hyperbolic triangle works like in the euclidean case.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
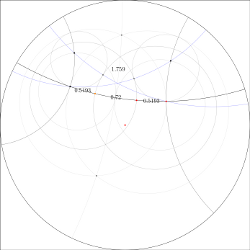
Golden ratio
The usual construction of the golden ratio fails. Mathematically, there exists a golden ratio,
but it can not be costructed this way.
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
Mirror circle
Mirroring a circle again and again along a line ...
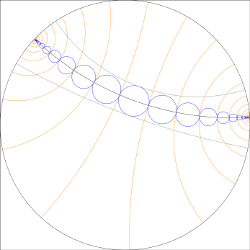 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
Hyperbolic regular pentagon
Two similar constructions of hyperbolic regular pentagons. Both constructions fail, as the
diagonals can not be constructed by means of the golden ratio as it is done in the euclidean case.
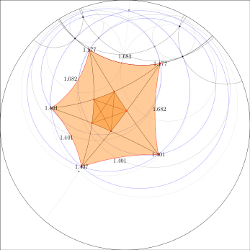 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
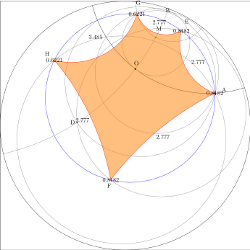 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file
Hyperbolic regular hexagon
The classical construction of an hyperbolic hexagon fails too. The well known formula U = 2*pi*r
for circles has to be modified for hyperbolic circles to U = 2*pi*sinh(r).
 Rendered as .pdf
Source as .asy file
Rendered as .pdf
Source as .asy file













